BAyeSian Interpretation of Estimates (BASIE)

Imagine that you are a policymaker and an academic researcher shows you evidence for a new health intervention that will dramatically improve health outcomes. He shows you the study results, the estimated impact and a p-value that is less than 0.05. How much credibility should you give to this result? What quantiative approach should you take to determine if the government should recommend using this new health intervention?

One approach for making this decision is the BAyeSian Interpretation of Estimates (BASIE) approach. BASIE was originally proposed in 2019 Mathematica Report (see other relevant papers at the end of this post). BASIE aims to estimate the probability that an intervention will have a meaningful effect, given the impact estimate and prior evidence regarding the effects of broadly similar interventions. The specific steps needed to implement BASIE are as follows.

For people familiar with Bayesian approaches, these steps should not be surprising. A key challenge when implementing a Bayesian approach is selecting a good prior. For education interventions, the paper recommends using the What Works Clearinghouse (WWC); in health, systematic literature reviews, Cochrane review or clinical guidelines could be useful starting points. When creating a prior, the authors caution to make sure populations are homogeneous, the estimates are adjusted for sample size, and the prior distribution is centered at 0.

When estimating the intervention effect, the authors recommend using both the traditional estimate (i.e., based on study data alone, with a p-value) and the shrunken estimate which shrinks this estimate towards the prior distribution.

When the shrunken estimates are used, one can also produce credible intervals based on the posterior distribution. Credible intervals are often considered the Bayesian approach to confidence intervals. However credible intervals should (i) only be interpreted relative to the selected prior distribution and (2) are not predictive statements about the effects in the future, but instead of retrospective statements about the effect of an intervention in the evaluation context. For instance, one could say that intervention X had a 90% chance of increasing survival by 10%, given the treatment trial and prior evidence from clinical trials of drugs in the same therapeutic class treating the same disease. One should also report the probability that the intervention’s effect exceeds that minimum meaningful effect size.

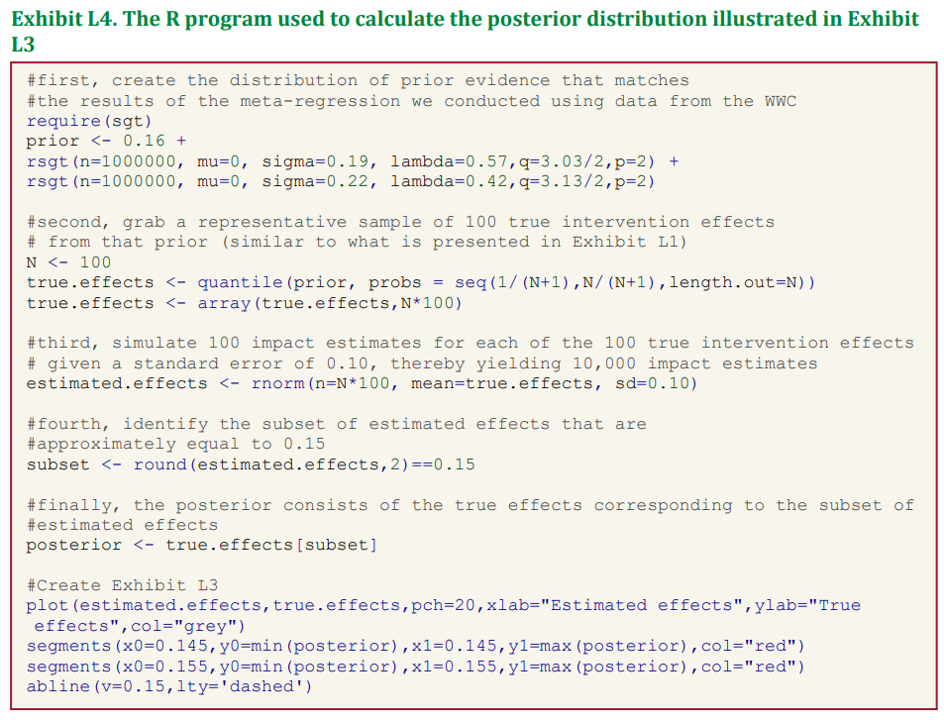
The report also has code in R to explain how to calculate posterior distributions, with the code below showing how to do this with a simple toy example. Although the BASIE approach is applied to an educational intervention approach, the same statistical approach could be used in health economics or any other scientific field.

Appendix

BASIE was largely derived from the following academic studies:

Gelman, A. (2011). Induction and deduction in Bayesian data analysis. Special topic issue, Statistical science and philosophy of science: Where do (should) they meet in 2011 and beyond? Rationality, Markets and Morals, 2, 67–78. Gelman, A. (2015, July 15). Prior information, not prior belief. http://andrewgelman.com/2015/07/15/prior-information-not-prior-belief/ Gelman, A. (2016, April 23). What is the “true prior distribution”? A hard-nosed answer. http://andrewgelman.com/2016/04/23/what-is-the-true-prior-distribution-a-hard-nosedanswer/ Gelman, A., & Hennig, C. (2017). Beyond subjective and objective in statistics. Journal of the Royal Statistical Society, Series A (Statistics in Society), 180(4), 967–1033. Gelman, A., & Shalizi, C. (2013). Philosophy and the practice of Bayesian statistics (with discussion). British Journal of Mathematical and Statistical Psychology, 66, 8–80.