Should we trust staggered difference-in-differences estimates?
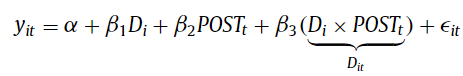
That is the question posed in paper by Baker, Larcker and Wang (2022). I summarize their key arguments below.
The validity of…[the DiD]…approach rests on the central assumption that the observed trend in control units’ outcomes mimic the trend in treatment units’ outcomes had they not received treatment. As the authors write:
First, DiD estimates are unbiased in settings with a single treatment period, even when there are dynamic treatment effects. Second, DiD estimates are also unbiased in settings with staggered timing of treatment assignment and homogeneous treatment effect across firms and over time. Finally, when research settings combine staggered timing of treatment effects and treatment effect heterogeneity, staggered DiD estimates are likely biased.
Oftentimes, DiD is implemented using an ordinary least squares (OLS) regression based model as follows:
When there are more than two groups and more than and 2 time periods, regression-based DiD models typically rely on two-way fixed effect (TWFE) of the form:
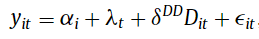
Where the first two coefficients are unit and time period
fixed effects. Note that previous research from Goodman-Bacon
(2021) shows that static forms of the TWFE DiD is actually a “weighted
average of all possible two-group/two-period DiD estimators in the data.”
When treatment effects can change over time (“dynamic
treatment effects”), staggered DiD treatment effect estimates can actually
obtain the opposite sign of the true ATT, even if the researcher were able to
randomize treatment assignment (thus where the parallel-trends assumption
holds).
The reason for this is because Goodman-Bacon
(2021) shows that the static TWFE DiD is actually consists of 3 components:
Variance-weighted average treatment effect on
the treated (VWATT)Variance-weighted average counterfactual trends
(VWCT)Weighted sum of the change in the average
treatment on the treated within a treatment-timing group’s post-period and
around a later-treated unit’s treatment window (ΔATT)
The first term is the term of interest. If the parallel trends occurs, then VWCT =0. The last term arises because, under static
TWFE DiD, already-treated groups as effectively used as comparison groups for later-treated
groups. If DiD is estimated in a
two-period model, however, this term disappears and there is no bias. Alternatively,
if treatment effects are static (i.e., not changing over time after the
intervention), then ΔATT = 0 and TWFE DiD is valid.
The challenges, however, occurs when treatment effects are
dynamic. In this case ΔATT
≠
0 and the TWFE DiD is biased.
So what can be done? The authors offer 3 solutions:
Callaway and Santa’Anna (2021). Here, the authors allow one to estimate treatment effect for a particular group (treatment at time g) using observations at time τ and g-1 from a clean set of controls. These are basically not-yet treated, last-treated, or never-treated groups. Sun and Abraham (2021). A similar methodology is used as in CS, but always-treated units are dropped, and the only units that can be used as effective controls are those that are never-treated or last-treated. Further, this approach is fully parametric.Stacked regression estimators. Cengiz (2019) implements this approach. The goal is to “create event-specific “clean 2 × 2” datasets, including the outcome variable and controls for the treated cohort and all other observations that are “clean” controls within the treatment window (e.g., not-yet-, last-, or never-treated units). For each clean 2 × 2 dataset, the researcher generates a dataset-specific identifying variable. These event-specific data sets are then stacked together, and a TWFE DiD regression is estimated on the stacked dataset, with dataset-specific unit- and time-fixed effects… In essence, the stacked regression estimates the DiD from each of the clean 2 × 2 datasets, then applies variance weighting to combine the treatment effects across cohorts efficiently.”
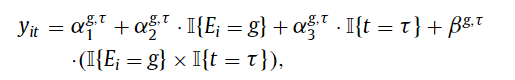
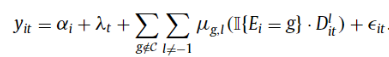
While there has been a lot of math in this post, if researchers apply these alternative DiD estimators, the authors wisely recommend that “researchers should justify their choice of ‘clean’ comparison groups—not-yet treated, last treated, or never treated—and articulate why the parallel-trends assumption is likely to apply”.
You can read the full article here.







